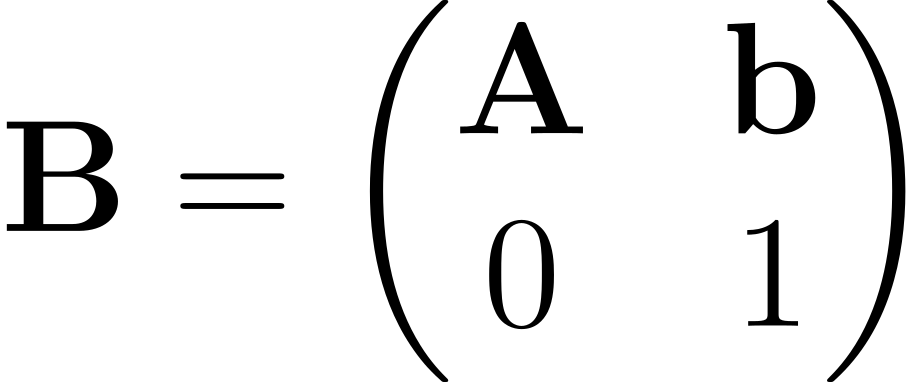Estimating the Security of Homomorphic Encryption Schemes
The security of any cryptography scheme is paramount. As part of our commitment to this, our team at Zama have been working on improving the Lattice Estimator. The Lattice Estimator (formerly the LWE Estimator) is a tool used throughout industry and academia to estimate the security level of Learning with Errors-based parameter sets. The tool has been used previously in standardization efforts: including the NIST standardization process for post-quantum encryption/signature schemes, as well as the ISO effort to standardize homomorphic encryption schemes.
The goal of our work is to bring the Lattice Estimator in-line with state-of-the-art attacks in the literature, so that users can be confident in the selection of their cryptographic parameters. Moreover, we are making this work public in line with our commitment to open-source projects.
Learning with Errors
The Learning with Errors problem challenges an adversary to recover a secret vector s from a noisy system of equations b = A*s + e, where A is a public integer matrix of size m x n, all the other terms are vectors such that the dimensions match and the arithmetic is modulo some modulus q. For this problem to be well-defined, we assume that n is smaller than m and that e is small.
With the correct selection of parameters, this problem can provide an assured level of security (such as 128-bits) for a wide range of cryptographic primitives, for example homomorphic encryption schemes, including Zama’s Concrete library. This is achieved by estimating the running times of known attacks, and setting the security level to be the running time of the fastest attack (optionally, with some additional security margin).
There are a bunch of attacks, as we will see below, and it is generally unclear which attack is the most efficient for a given instance. As pointed out in the work that initiated the LWE estimator, for each attack there are LWE instances (i.e. values of m, n, q, and size of e) for which this attack is the fastest. So unless you have really good intuition for specific LWE parametrizations, estimating the security of an LWE instance requires checking all known attacks. Performing this step manually for every possible instantiation of a scheme (or every new scheme) quickly becomes tedious, especially since many attacks have several parameters that need to be optimized. This is where the estimator comes in: it provides an automated way of quickly estimating the running time of all major attacks against an LWE challenge, just given the parameters of the problem. It thus allows a user to quickly evaluate the security of a specific parametrization of e.g. an encryption scheme based on LWE.
Attacks
Let’s now look at a subset of the attacks considered in the Lattice Estimator. In particular, we’ll discuss the class of lattice attacks comprising the uSVP attack, decoding attacks, and dual attacks. We present simplified versions of these attacks for the purposes of this blog post, further details can be found e.g. here. Before we dive into the attacks, a reminder that lattices are discrete subgroups of Rⁿ.
The uSVP Attack
The uSVP attack constructs a lattice L for which the LWE error vector (i.e (e,1)) is an unusually short vector in L. This lattice has basis matrix B, where:
We can see that this lattice contains the short vector (e,1) by considering the argument:
We can then use known approximation algorithms (i.e. lattice reduction techniques) to recover this secret vector, at a known cost. The shorter the secret vector, i.e. the more unusual, the lower the cost of recovering it. Once the error vector e is recovered, we can easily find the LWE secret s via Gaussian elimination.
Decoding Attacks
Decoding attacks succeed via the construction of Bounded Distance Decoding (BDD) instances. The figure below shows how this looks for LWE. We have a lattice generated by the public LWE matrix A, which contains the (private) lattice point (s, As). This private lattice point is separated from the public point t = (0,b), by the (private) vector (s,-e). This is exactly a BDD instance: we know b (as it is public), and we want to find the closest lattice point (i.e. (s, As)) in order to recover the vector (s,-e). Notice that it is important here that s and e are short, since otherwise we may find the incorrect lattice vector.
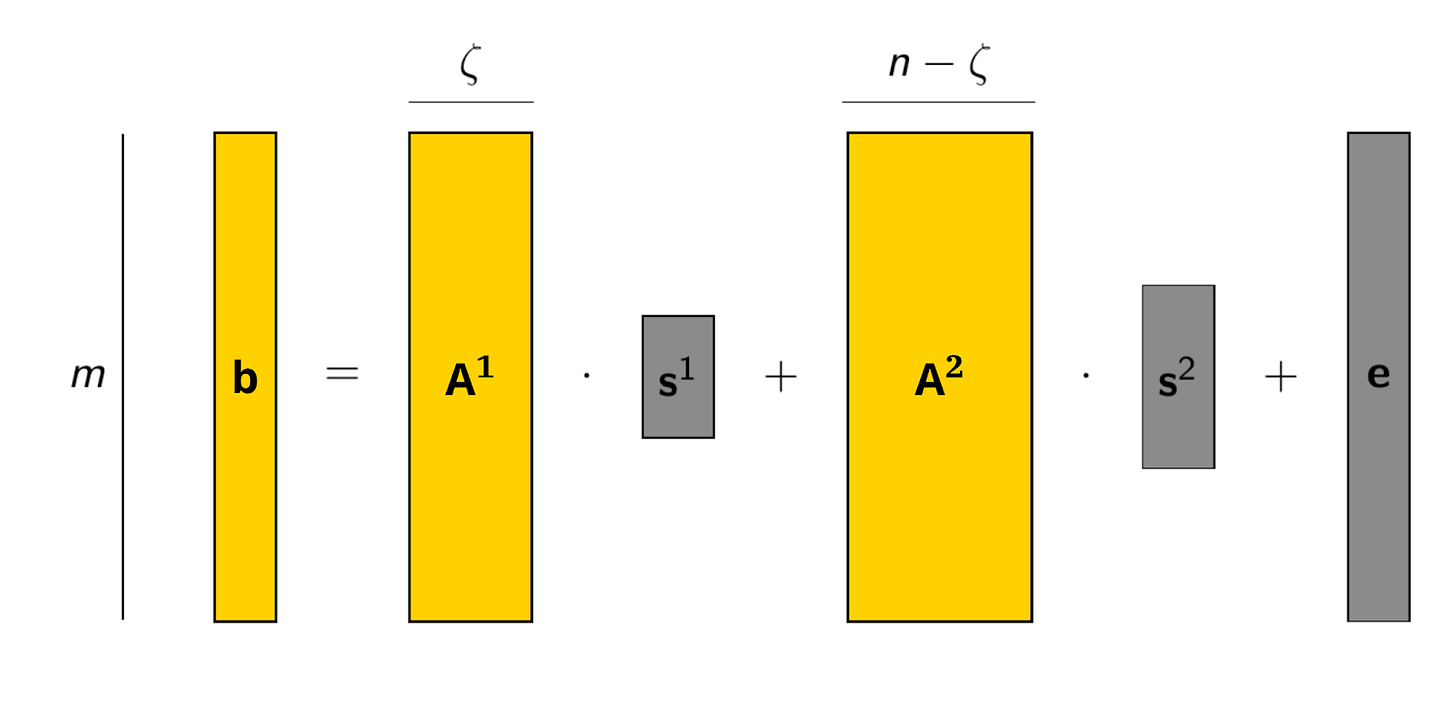
The decoding attack can be improved (for certain parameters) by combining this approach with some searching strategy, which is known as a so-called (primal) hybrid attack. Specifically, we can break up the matrix A = [A¹ | A²] and the secret s = (s¹ | s²), and then write b = A*s + e = A¹*s¹ + A²*s² + e. Assume s¹ has length 𝛇 and, by some lucky coincidence, we happen to know s¹. Then we can “remove” that part of the secret by computing b’ = b — A¹*s¹ = A²*s² + e.
This instance is easier to solve, since the secret is smaller. But how would we come to know s¹? One option is to simply guess it. So we could search through all possible candidates for s¹ and try to solve the corresponding smaller LWE instance. It’s not immediately clear that reducing the size of the LWE problem is worth the additional effort of searching through all candidates for s¹, but we can take advantage of the fact that these new instances are not independent: they all have the same public matrix A², which allows to amortize some heavy precomputation and thus improve the attack. This approach can be improved further, by employing some Meet-In-The-Middle techniques to speed up the exhaustive search part.
Dual Attacks
The dual attack is a little less direct than the previous two approaches. The main idea is to find some vector v such that v*A = 0 and v is short, i.e. only has small entries. If we are able to find such a vector, we can multiply the challenge vector b with it (a.k.a. take the inner product) to obtain v*b = v*A*s + v*e = v*e. Since e is typically a short vector and we know that v is short as well, this inner product should also be small.
You might be wondering how this is useful since it is not clear at first glance how this helps us solve the challenge of finding s. Notice though that this allows us to tell with some confidence if b is a properly formed LWE vector (with respect to the given public matrix A) or if it is just random junk, since random junk is unlikely to be small (even after multiplication with v). As it turns out, this is enough to break the security of encryption schemes based on the LWE problem. (You can also use this distinguishing algorithm to actually find the secret s with some more effort, but as stated, this is not actually required.) The hard part of this approach is to find a short vector v satisfying the above constraints.
This is an instance of a lattice problem and we can use our old friend, lattice reduction, to tackle this. The shorter the vector we find the better we can distinguish and thus the better the success probability of the attack, but finding short vectors in a lattice is hard. Optimising this trade-off is something the estimator can do for you.
As for primal hybrid attacks, we can again break up the problem at hand and use the dual attack to solve only part of it, which will yield dual hybrid attacks. More specifically, we break up the matrix A = [A¹ | A²] and the secret s = (s¹ | s²) again and write b = A*s + e = A¹*s¹ + A²s² + e. It is easier to find a short vector v such that v*A¹ = 0, because the lattice corresponding to A¹ has a smaller dimension and volume compared to A. If we now multiply this vector with b, we get b’ = v*b = v*A²*s² + v*e. Notice that we can also compute a’ = v*A². Accordingly, we can view (a’, b’) as a row of a new LWE instance with smaller secret s² but larger noise. Using multiple such vectors v we can compute more rows of such an instance and hence a new LWE problem. For this new problem, we can use any other suitable attack, for example exhaustive search or Meet-In-The-Middle attacks. Again, we need to optimize over several parameters, for example the point where we split the matrix. With our PR to the Lattice Estimator, it can handle such attacks and optimize over all attack parameters.
Our Work
Put simply, what we’ve done is to bring the estimations for several attacks in the Lattice Estimator up to speed so they now represent the state-of-the-art. For this we focused mainly on hybrid attacks, because 1) this is where the estimator had the largest gaps and 2) these are particularly relevant for LWE instances that come up in FHE. Full technical details can be found in the associated pull request on the Lattice Estimator repository. The following table summarizes our contributions.
Retrieving Security Estimates
To show why the improvements outlined in Table 1 are important, we present some security estimates where the hybrid-dual and hybrid-decoding approaches are the fastest attacks and thus determine the security level of the LWE instance. Ignoring these attacks would likely result in overestimates of the security level, which is never the side you want to err on.
We demonstrate the power of the hybrid attacks using example parameter sets from this work. These parameters have not actually been proposed for use in any scheme, but they are close to what you might use in an FHE scheme and are useful for benchmarking and comparison. In fact, some of these sets are not too far off from what Concrete is using for some parts, with the main difference being that the secret in Concrete is binary and uniform, while in these examples it is ternary and sparse. Using sparse secrets may yield favorable trade-offs between security and performance, and some schemes do use sparse secrets for that reason, but accurate security estimation is paramount here.
We start with a parameter set where the secret dimension n=1024 and the modulus is q=2²⁵, and the standard deviation of the error distribution is σ=3.2. As part of this process, we have to select a model for estimating the running time of lattice reduction. While the default in the Lattice Estimator is a model from the Kyber submission to the NIST PQC, we use the BDGL16 estimate, which is more common in the literature (and used in previous efforts for HE standardization). Calling the Lattice Estimator via estimate_lwe() on this parameter set produces an output of the form:
dual : rop: ≈2^145.8, mem: ≈2^80.5, m: 915 ...dual_hybrid : rop: ≈2^114.6, mem: ≈2^92.3, m: 637 ...dual_mitm_hybrid : rop: ≈2^124.5, mem: ≈2^96.5, m: 637 ...primal_bdd : rop: ≈2^129.6, red: ≈2^129.5, ...primal_usvp : rop: ≈2^131.9, red: ≈2^131.9, ...primal_hybrid : rop: ≈2^110.0, red: ≈2^109.0, ...For a user, the important thing to notice is the rop value, i.e. “ring-operations”. Roughly speaking, this value corresponds to the time taken for the corresponding attack to be successful. We set the security of the parameter set according to the fastest attack, i.e. the attack with the smallest rop value. In this example, the fastest attack is primal_hybrid with a running time of 2¹¹⁰ ring-operations. Therefore, we say that this parameter set has a security level of 110-bits.
Now assume that for our application the noise grows too much for this parameter set to work, which is a common situation to arise in noisy homomorphic encryption. There are several ways to address this, one of them might be to increase the modulus (while keeping the size of the noise e the same). This naturally results in a decrease in security, which you can compensate for by using a larger dimension n. So let us try to set q=2⁸² and n=4096. The hope would be that this might maintain the security level. To check this, we again run the estimator, which gives the following output.
dual : rop: ≈2^175.0, mem: ≈2^95.6, m: ≈2^11.9 ...dual_hybrid : rop: ≈2^123.5, mem: ≈2^92.5, m: ≈2^11.1 ...dual_mitm_hybrid : rop: ≈2^113.7, mem: ≈2^84.6, m: ≈2^11.0 ...primal_bdd : rop: ≈2^168.3, red: ≈2^168.1, ...primal_usvp : rop: ≈2^169.0, red: ≈2^169.0, ...primal_hybrid : rop: ≈2^114.7, red: ≈2^113.9, ...As we can see from the output, we indeed are able to maintain the level of security. What is interesting is that the most efficient attack actually switched from being the primal hybrid attack, to dual hybrid attack (using Meet-In-The-Middle techniques).
Summary
Tools like the Lattice Estimator are vital to ensure that homomorphic encryption schemes are deployed in a secure manner. We plan to continue our contributions to the Lattice Estimator to ensure that the community can have additional confidence in the security of their homomorphic encryption parameter sets.
We are hiring! Join Zama and help us safeguard privacy by making the internet encrypted end-to-end. All the info here: jobs.zama.ai
We’re open source — follow Zama’s Concrete library on Github here: github.com/zama-ai